52Heartz's Blog

分享科技与生活

发表于 更新于

最近有篇文章在引用中嵌套代码块，在 Typora 编辑器和博客的 NexT 主题中显式效果不一样，所以特地深入探究了一下。

以下测试效果基于 Hexo 3.8.0 、NexT 主题 NexT.Gemini v6.6.0。

会出问题的写法

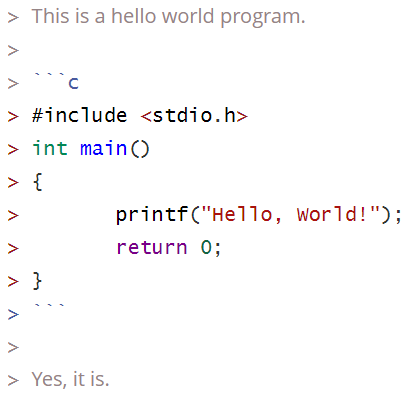
wrong-sourcecode

错误写法的源代码

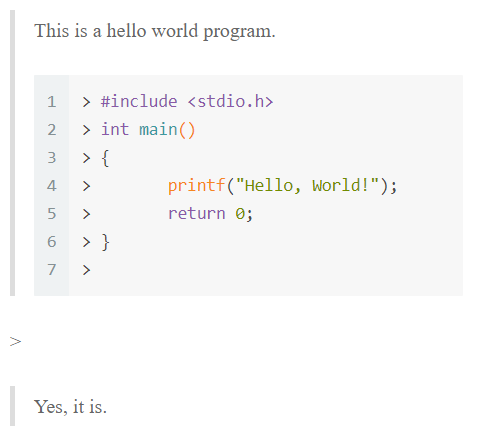
wrong-preview-in-hexo

错误写法在 Hexo 中的渲染

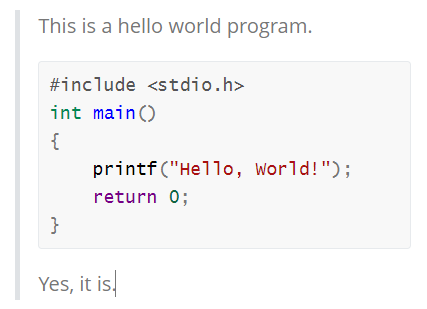
wrong-preview-in-typora

错误写法在 Typora 中的渲染

问题

显示效果

Hexo Typora
是否正常 不正常，有多余的 >，代码块和下一段文本中间会断开 正常
是否有代码块效果 有 有
是否有行号 有 有
是否有配色 有 有

正确的写法

正确写法1：使用 Hexo 特定代码块写法

right-1-sourcecode

正确写法1的源代码

right-1-preview-in-hexo

正确写法1在 Hexo 中的渲染

right-1-preview-in-typora

正确写法1在 Typora 中的渲染

需要注意的一个地方

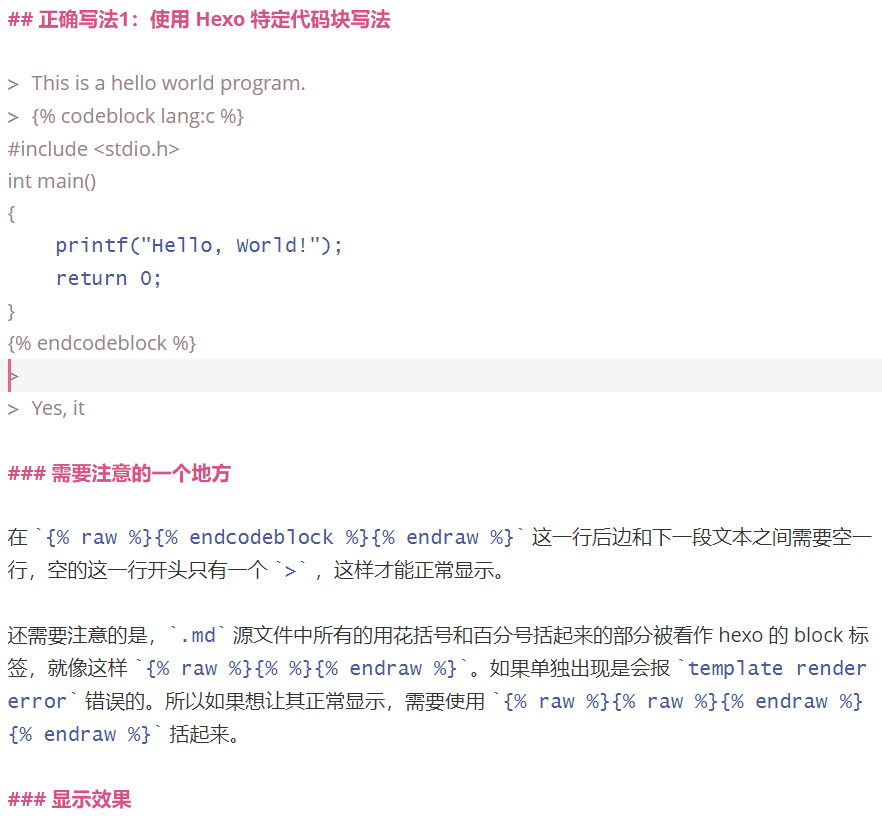
在 {% endcodeblock %} 这一行后边和下一段文本之间需要空一行，空的这一行开头只有一个 > ，这样才能正常显示。

还需要注意的是，.md 源文件中所有的用花括号和百分号括起来的部分被看作 hexo 的 block 标签，就像这样 {% %}。如果单独出现是会报 template render error 错误的。所以如果想让其正常显示，需要使用 {% raw %}{% endraw %} 括起来。如下所示：

right-1-a-problem

显示效果

Hexo Typora
是否正常 正常 不正常
是否有代码块效果 有 无
是否有行号 有 无
是否有配色 有 无

  • 相关代码：

    1
    2
    {% codeblock %}
    {% endcodeblock %}

正确写法2：多四个空格

在引用的文本中，在某一行的前边比其他行的开头多打 4 个空格，这一行在 Hexo 中会自动变为代码块显示。

right-2-sourcecode

正确写法2的源代码

right-2-preview-in-hexo

正确写法2在 Hexo 中的渲染

right-2-preview-in-typora

正确写法2在 Typora 中的渲染

显式效果

Hexo Typora
是否正常 正常 不正常
是否有代码块效果 有 无
是否有行号 无 无
是否有配色 无 无

正确写法3：代码块中不使用 >

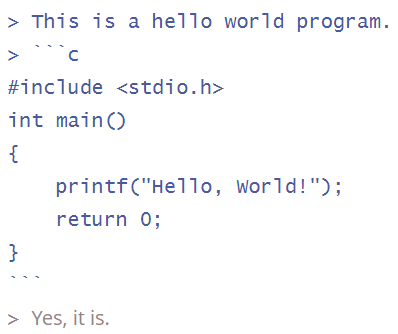
right-3-sourcecode

正确写法3的源代码

right-3-preview-in-hexo

正确写法3在 Hexo 中的渲染

⚠ 如果使用 Typora 编辑器，需要注意

Typora 编辑器中，只能在源代码模式下进行这样的编辑，但是一旦退出源代码模式，Typora 就会自动给很多行前边都加上 >，还会在每行前边都加上很多空格。所以，除非直接在源代码模式下编辑之后不再退出源代码模式，才能保证显示效果。

显示效果

Hexo Typora
是否正常 正常 不正常，且会导致其他部分不正常显示
是否有代码块效果 有 无
是否有行号 有 无
是否有配色 有 无

参考文章

  1. Hexo 异常 - Template render error unexpected token
  2. Hexo博客Bug：“{{”符号引起的生成报错
  3. Hexo的一个小BUG(Template render error)
  4. hexo 在markdown文档中出现 {% %} 语法会报错，提示“Template render error: (unknown path) ” #3346

发表于 更新于 分类于

使用 System.NanoTime()

System.NanoTime() - Java Docs

1
public static long nanoTime()

Returns the current value of the running Java Virtual Machine’s high-resolution time source, in nanoseconds.

This method can only be used to measure elapsed time and is not related to any other notion of system or wall-clock time. The value returned represents nanoseconds since some fixed but arbitrary origin time (perhaps in the future, so values may be negative). The same origin is used by all invocations of this method in an instance of a Java virtual machine; other virtual machine instances are likely to use a different origin.

This method provides nanosecond precision, but not necessarily nanosecond resolution (that is, how frequently the value changes) - no guarantees are made except that the resolution is at least as good as that of currentTimeMillis().

Differences in successive calls that span greater than approximately 292 years ($2^{63}$ nanoseconds) will not correctly compute elapsed time due to numerical overflow.

The values returned by this method become meaningful only when the difference between two such values, obtained within the same instance of a Java virtual machine, is computed.

For example, to measure how long some code takes to execute:

1
2
3
long startTime = System.nanoTime();
// ... the code being measured ...
long estimatedTime = System.nanoTime() - startTime;

To compare two nanoTime values

1
2
3
long t0 = System.nanoTime();
...
long t1 = System.nanoTime();

one should use t1 - t0 < 0, not t1 < t0, because of the possibility of numerical overflow.

  • Returns:

the current value of the running Java Virtual Machine’s high-resolution time source, in nanoseconds

  • Since:

1.5

示例

1
2
3
4
5
6
7
8
9
long startTime;
long durationNanoSecond;
double durationMilliSecond;

startTime = System.nanoTime();
doSomething();
durationNanoSecond = System.nanoTime() - startTime;
durationMilliSecond = durationNanoSecond / 1_000_000;
System.out.println("time:" + durationMilliSecond);

使用 System.currentTimeMillis()

1
public static long currentTimeMillis()

Returns the current time in milliseconds. Note that while the unit of time of the return value is a millisecond, the granularity of the value depends on the underlying operating system and may be larger. For example, many operating systems measure time in units of tens of milliseconds.

See the description of the class Date for a discussion of slight discrepancies that may arise between “computer time” and coordinated universal time (UTC).

  • Returns:

    the difference, measured in milliseconds, between the current time and midnight, January 1, 1970 UTC.

  • See Also:

    Date

示例

1
2
3
4
long startTime = System.currentTimeMillis();
doSomeThing();
long duration = System.currentTimeMillis() - startTime;
System.out.printf("[Duration]%d ms", duration);

可能的误差

System.currentTimeMillis() 在部分 Windows 系统中可能存在 10ms 的误差。有人说在他的游戏程序中使用 nanoTime() 之后比使用 currentTimeMillis() 的时候游戏画面过渡更平滑。

参考资料

  1. System.NanoTime() - Java Docs
  2. System.currentTimeMillis vs System.nanoTime - Stack Overflow
  3. java中的System.nanoTime与System.currentTime - 博客园
  4. How to convert nanoseconds to seconds using the TimeUnit enum? - Stack Overflow
  5. 使用System.nanoTime测试代码执行时间

发表于 更新于

今天面试遇到的一道题。与参考资料的第一篇文章类似。

另外可以参考STL源码中 rotate() 函数的实现思路。

//TODO 有待填坑

测试几种算法的运行效率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
public class Solution {

    //rotate_right
    public static void tripleReverse(int[] nums, int K) {
        int length = nums.length;
        reverse(nums, 0, length - K - 1);
        reverse(nums, length - K, length - 1);
        reverse(nums, 0, length - 1);
    }

    private static void reverse(int[] nums, int start, int end) {
        int sum = start + end;
        int temp;
        for (int i = start; i <= (start + end) / 2; ++i) {
            temp = nums[i];
            nums[i] = nums[sum - i];
            nums[sum - i] = temp;
        }
    }

    //rotate_right
    public static void doubleSwap(int[] nums, int K) {
        int start = 0;
        int end = nums.length;
        int middle = nums.length - K;
        int i = middle;
        int temp;

        while (true) {
            temp = nums[start];
            nums[start] = nums[i];
            nums[i] = temp;
            ++start;
            if (++i == end) {
                if (start == middle) {
                    break;
                }
                i = middle;
            } else if (start == middle) {
                middle = i;
            }
        }
    }

    // rotate left
    // if want to rotate right, add [K = nums.length - K] at the beginning
    public static void rotate_GCD(int nums[], int K) {
        int length = nums.length;
        int front, post, temp;
        for (int i = 0; i < GCD(length, K); ++i) {
            temp = nums[i];
            front = i;
            while (true) {
                post = front + K;
                if (post >= length) {
                    post = post - length;
                }
                if (post == i) {
                    break;
                }
                nums[front] = nums[post];
                front = post;
            }
            nums[front] = temp;
        }
    }

    private static int GCD(int a, int b) {
        if (b == 0) {
            return a;
        } else {
            return GCD(b, a % b);
        }
    }

    public static void main(String[] args) {
        // 一亿个整数，大概需要三百多兆的内存
        int[] array = new int[1_0000_0000];
        for (int i = 0; i < 1_0000_0000; ++i) {
            array[i] = i;
        }

        long startTime;
        long durationNanoSecond;
        double durationMicroSecond;

        startTime = System.nanoTime();
        tripleReverse(array, 1000000);
        durationNanoSecond = System.nanoTime() - startTime;
        durationMicroSecond = durationNanoSecond / 1_000;
        System.out.println(String.format("[tripleReverse]Time:%f 微秒",
        durationMicroSecond));

        startTime = System.nanoTime();
        doubleSwap(array, 1000000);
        durationNanoSecond = System.nanoTime() - startTime;
        durationMicroSecond = durationNanoSecond / 1_000;
        System.out.println(String.format("[doubleSwap]Time:%f 微秒", durationMicroSecond));

        startTime = System.nanoTime();
        rotate_GCD(array, 1000000);
        durationNanoSecond = System.nanoTime() - startTime;
        durationMicroSecond = durationNanoSecond / 1_000;
        System.out.println(String.format("[rotate_GCD]Time:%f 微秒", durationMicroSecond));

        System.out.print("[result]");
        for (int i = 0; i < 10; i++) {
            System.out.printf("%d,", array[i]);
        }
    }
}

参考资料

  1. 数组循环移位，你能想到多少种算法？
  2. STL源码—— rotate算法理解
  3. STL实现细节之rotate()
  4. 《STL源码剖析》学习–6章–_rotate算法分析
  5. STL源码之rotate函数结合图和实例分析
  6. Permutation Algorithms - From Mathematics to Generic Programming (2015)
  7. Program for array rotation

发表于 更新于 分类于 ，

题目来源：53. Maximum Subarray - LeetCode

题目难度：Easy

题目

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

1
2
3
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

解答1[Java]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length <= 0)
            return 0;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int max = dp[0];

        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
            max = Math.max(max, dp[i]);
            max = dp[i] > max ? dp[i] : max;
        }
        return max;
    }
}

思路

动态规划。dp[i] 中存储的是 i 之前的最大的子序列和。

时间复杂度 $O(n)$，空间复杂度为 $O(n)$。

解答2[Java]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int maxSubArray(int[] nums) {
        int maxSum = nums[0];
        int curSum = 0;

        for (int n : nums) {
            curSum += n;
            if (curSum > maxSum) {
                maxSum = curSum;
            }
            if (curSum < 0) {
                curSum = 0;
            }
        }

        return maxSum;
    }
}

思路

一直加，用 curSum 表示截至目前的最大正子序和。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

0%